Union-Find算法
在一个连通网络中,如果存在链路,使得一个节点能通过这条链路到达另一个节点,那么我们就说这两个节点之间是连通的。在连通性问题中,通常需要判断给定的两个节点是否已经连通,这个过程称为查找(find)操作,此外,若两个点并没有连通,我们可以创建连通这两个节点的链路,从而使得这两个节点处于连通状态,这个过程称为合并(union)操作。在执行合并操作之后,网络处于新的连接状态,这时,我们就可以根据更新后的网络的状态,来判断给定的其它两个节点之间是否连通了。
为了简化处理,我们可以使用整数来给网络中的节点进行编号。首先,我们给出一个测试程序,程序每次都会要求用户输入一对整数,并且执行以下操作:
- 判断这对整数代表的节点是否处于连通状态,这就是查找操作。
- 若这两个点没有连通,那么执行合并操作,使得这两个点处于连通状态。 12345678910111213141516171819202122using namespace std;int main(){UnionFind uf(10000); // 10000 nodesint p, q;while (cin >> p >> q){if (uf.find(p, q)){cout << "connection " << p << "-" << q << " already exist!" << endl;}else{uf.unite(p, q);cout << "new connection: " << p << "-" << q << endl;}}return 0;}
我们可以使用简单的输入来测试程序,输入的两个整数代表两个节点,若这两个节点尚未连通,那么程序就会负责连通这两个点,若这两个点已经连通,则输出提示信息:
我们可以用下图1.1来表示对节点执行合并操作的过程,从中可以看到,节点之间的连通是具有传递性,最后,图中的5个节点都处于互通的状态: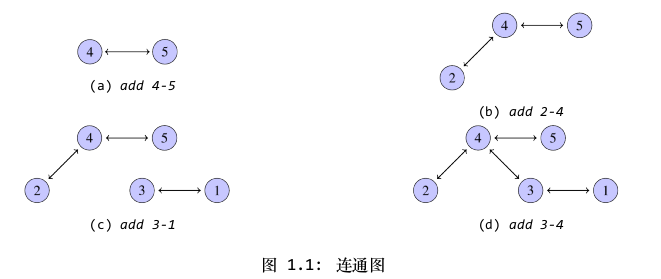
Quick-Find算法
在Quick-Find算法中,我们使用数组来表示所有节点的集合,在一开始,数组中的元素的值各不相同,这表示所有的节点均不连通,很显然,要是数组中存在相同的元素值,那么就表示这些元素所代表节点是互通的。由此,判断两个节点是否连通(即查找操作)就变得相当简单,只需要判断数组中的这两项元素的值是否相同,相同就表示它们是连通的。此外,要是这两个节点(假设为A节点和B节点)并不连通,那么就要执行合并操作,这时我们需要遍历整个数组,使得所有与A节点连通的节点都与B节点连通。
Quick-Find算法中,查找操作的复杂度为O(1),而合并操作的复杂度为O(N),N表示数组的长度,即所有节点的数目。
图1.2表示了Quick-Find算法合并节点的过程,需要注意,节点中的数字表示节点的编号(即数组元素的下标),而不是数组元素的值。执行一次合并操作,我们需要遍历所有节点。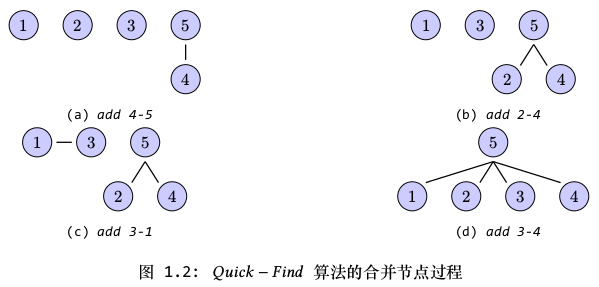
Quick-Union算法
在Quick-Union算法中,同样使用数组来表示所有节点,数组的下标表示节点的编号。但每个节点可以指向同一连通集中的另一节点,例如,假定arr[1]的值为2,那么就表示编号为1的节点指向编号为2的节点,那么这两个节点就是连通的。
如果节点指向其它的节点,我们可以顺着这条链路找到链路的最后一个节点,最后的这个节点将指向其自身。根据这个原理,我们可以发现,如果两个节点处于同一个连通集中,那么我们顺着这两个节点指向的链路,最后到达的将是同一个节点,由此可以判断两个节点是否处于同一个连通集中(连通集中的所有节点两两之间直接地或间接地连通)。
在Quick-Union算法中,判断两个节点是否处于同一个连通集,我们需要遍历两个节点所在的链路,同样,要是两个节点并不在同一个连通集中,则需要执行合并操作,例如,节点1和节点2处于同一连通集,节点3和节点4处于同一连通集:
为了合并两个节点,使得这两个节点处于同一连通集,我们需要分别顺着这两个节点所在的链路遍历到链路的最后一个节点,并且使其中一个节点指向另外一个节点。例如,假定我们需要合并节点1和节点4,由于节点2和节点3分别是两条链路的最后一个节点,那么我们可以让节点2指向节点3,这样,4个节点就将处于同一个连通集:
从节点1和节点4分别进行遍历,那么节点3就成为这两条链路共同的最后一个节点。由此可得,只要顺着两个节点所在的链路分别遍历到最后一个节点,再判断链路末端的两个节点是否是同一个节点,我们就可以轻易判断任意两个节点是否处于同一连通集了。
图1.3表示Quick-Union算法合并节点的过程。实际上,链路的最后一个节点可以看成是树的根节点,这个节点将指向其自身,以此,可以将整个连通集看成是一棵树,由于顺着同一连通集中的所有节点向上遍历,那么最后都会到达根节点,据此可判断任意两个节点是否处于同一棵树中(也即同一连通集中)。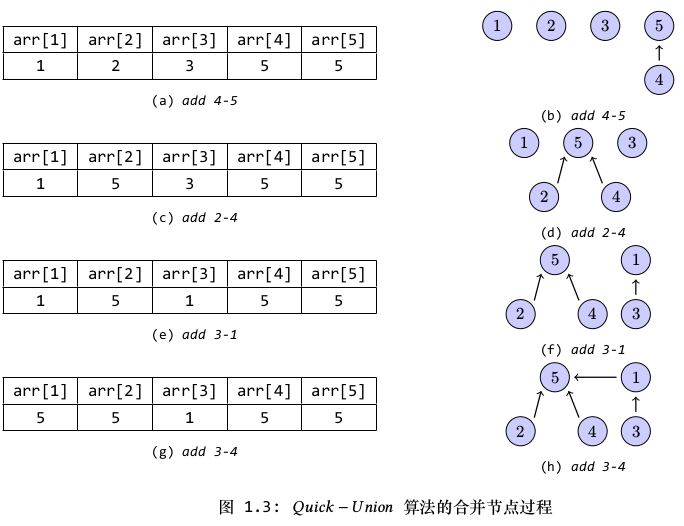
与Quick-Find算法相比,Quick-Union算法的合并操作并不需要遍历整个数组,因此显得相对快一些。为了分析Quick-Union算法的性能,我们需要考虑最坏的情况,在最坏的情况下,Quick-Union算法所形成的树将呈直线形状。例如,假定我们运行前面的测试程序,输入以下内容:
那么此时将形成图1.4所示的直线状的树:
此时,每次若需要查找节点0,我们就需要对直线状的树遍历一次。如果根据这种方式构建出一颗具有N个节点的直线树,那么平均每次需要执行的遍历操作次数为:
$$
T = \frac{0+1+2+ \cdots + (N-1)}{N} = \frac{N-1}{2}
$$
按照这种方式构造出具有N个节点的直线状的树,那么我们需要输入N对整数,总的遍历操作次数为:
$$
T_{total} = \frac{N(N-1)}{2}
$$
Weighted Quick-Union算法
在合并两棵树的过程,我们是使一棵树的根节点指向另一棵树的根节点,这时可以选择将大树连接到小树上,也可以将小树连接到大树上。图1.5表示了这个过程。这时我们可以发现,要是将大树连到小树,那么合并之后的树的高度将会增加1,而要是将小树连接到大树上,那么合并后的树的高度将不变。
为了防止Quick-Union算法出现最坏情况,在合并两棵树的过程,我们需要尽量阻止树的高度增加。为此,可以为每棵树增加一个计数器,用来存储树的节点数目,在合并两棵树时,就可以通过判断两棵树的节点数目,从而将小树连接到大树上,尽量阻止树高度的增加。这种算法就称为Weighted Quick-Union算法。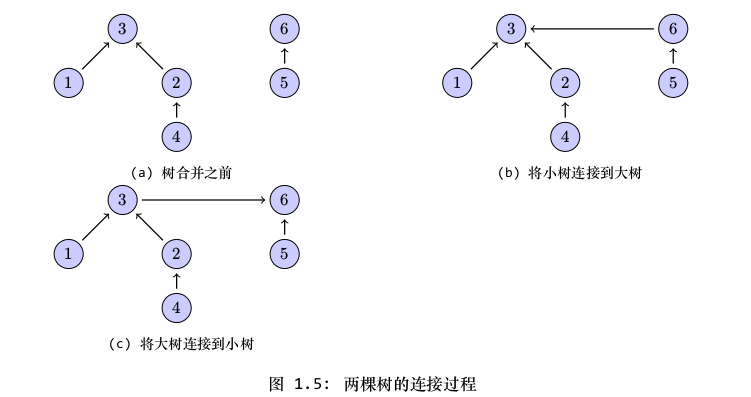
使用Weighted Quick-Union算法,在最坏情况下,假定树总共有$2^N$个节点,那么我们从任意叶节点开始,最多需要N次遍历就能到达根节点,实际上判断两个节点是否存在于同一棵树中的操作的其时间复杂度为O(log N)。
假定存在两棵树A和B,其节点数分别为$N_1$和$N_2$,且$N_1 \leq N_2$,对A和B进行合并,那么在合并之后,通常A的高度将会增加1,而B的高度将保持不变,合并之后的树总节点树为$N_1+N_2$。可以证明,在合并后的树中,从任意叶节点到达根节点,最多需要$\log(N_1+N_2)$次操作,因为$1+\log N_1 = \log(N_1+N_1) \leq \log(N_1+N_2)$。
路径压缩的Weighted Quick-Union算法
在Weighted Quick-Union算法所形成的树,只有少量的节点远离根节点,实际上这个算法非常高效,但我们还可以做得更好。在Weighted Quick-Union算法中,从叶节点遍历到根节点,在最坏情况下是O(log N)时间操作,我们可以对此进行改进,使得这个操作接近常量时间。
当从叶节点开始遍历到根节点的过程中,我们可以改变每两个节点中其中一个节点的指向,使其指向其前面的第二个节点,从而使路径缩短一半。正如图1.6所示,我们对直线形状的树执行折半路径压缩之后,路径缩短了将近一半,从而使树的高度减小,使树变得更扁平。
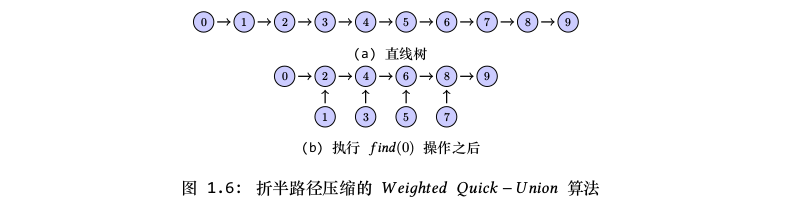
除了折半路径压缩算法之外,还可以使用完全路径压缩算法。假定我们从叶节点遍历到根节点的过程中,能使所有的节点都指向根节点,那么整棵树将变得更加扁平,这种方法称为完全路径压缩。
图1.7显示了使用这个算法来合并节点的过程,在树中顺着叶节点遍历到根节点的过程中,会使得路径中的所有节点直接与根节点连接,从而使树变得更加扁平。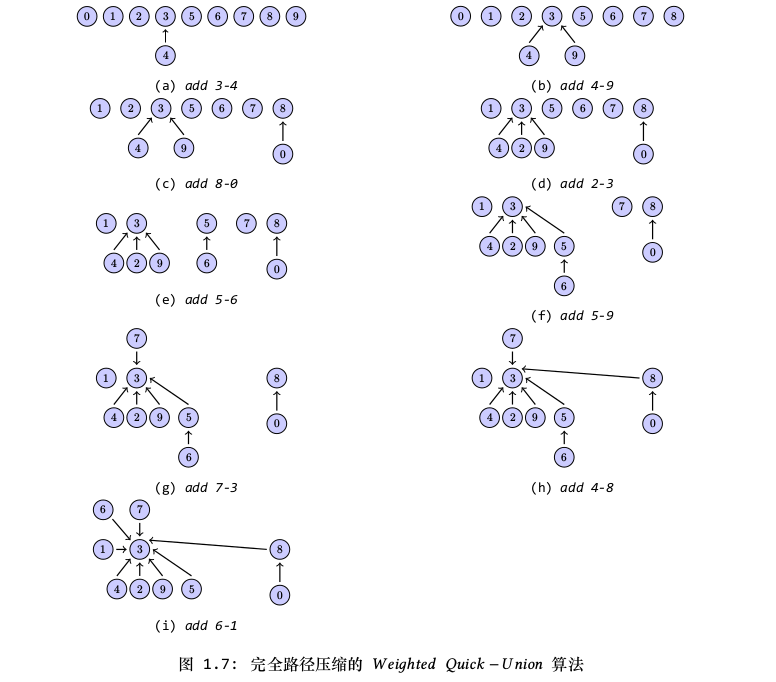
尽管通过路径压缩使得整棵树变得更加扁平,但却需要执行了一下额外的操作,实际上Weighted Quick-Union算法与路径压缩的Weighted Quick-Union算法相比,执行性能非常接近。