多项式算法的实现

发表于   |   分类于   |   阅读次数

　　在数值计算中，有时我们需要对多项式进行相加或相乘，此外，还经常需要对多项式进行求值。例如，假定我们需要对两个多项式进行乘法运算：
$$
(1+x+\frac{x^2}{2}-\frac{x^3}{6}) (1+x+x^2+x^3)= 1 + \frac{x^2}{2} + \frac{x^3}{3} - \frac{2x^4}{3} + \frac{x^5}{3} - \frac{x^6}{3}
$$

多项式的表示

　　我们可以定义一个Poly类用来表示多项式，在Poly中，我们使用数组来存储多项式的系数，由于系数作为数组的元素，那么系数对应的下标就是多项式的幂，例如，假定我们使用Poly来表示多项式$5+10x+8x^2+20x^4$，那么数组的结构就如下图所示：

　　我们可以用Poly来表示多项式，例如，我们可以用Poly<int>(2, 2)来表示$2x^2$，当然，我们可以通过全局函数plus()来组合多项式，例如：

1
auto poly = plus(Poly<double>(0.5, 2), Poly<double>(9.9, 4));

　　那么，可以看到，poly就可以用来表示$0.5x^2 + 9.9x^4$，这时，若需要对多项式进行求值，例如，令$x=2$，那么可以使用Poly的成员函数evaluate()来进行求值：

1
std::cout << poly.evaluate(2) << std::endl;　　　　　　　　　    // print 160.4

　　下面给出Poly的具体实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <vector>
template <typename T>
class Poly
{
    template <typename Type>
    friend Poly<Type> plus( const Poly<Type> &, const Poly<Type> & );
    template <typename Type>
    friend Poly<Type> multiply( const Poly<Type> &, const Poly<Type> & );
    template <typename Type>
    friend std::ostream &operator<<( std::ostream &, const Poly<Type> & );
public:
    Poly( T coefficient, int power )
        : size_{ power + 1 }, arr_( size_, T{ 0 } ) {
            arr_[power] = coefficient;
    }
    
    double evaluate( double value ) const;
private:
    int size_;
    std::vector<T> arr_;
};
template <typename T>
std::ostream &operator<<( std::ostream &os, const Poly<T> &poly ) {
    for( int i = 0; i < poly.size_; ++i ) {
        if( poly.arr_[i] != 0 ) {
            os << poly.arr_[i] << "x^" << i 
               << ( i != poly.size_ - 1 ? " +" : "" ) << " ";   
        }
    }
    return os;
}

多项式的加法

　　在对多项式进行加法运算时，我们需要对幂相同的项系数进行累加：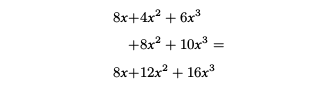　　

　　plus()函数实现多项式的加法：

1
2
3
4
5
6
7
8
9
10
11
12
13
template <typename T>
Poly<T> plus( const Poly<T> &first, const Poly<T> &second ) {
    int maxPower = std::max( first.size_ - 1, second.size_ - 1 );
    Poly<T> newPoly( T{ 0 }, maxPower );
    for( int i = 0; i < first.size_; ++i ) {
        newPoly.arr_[i] += first.arr_[i];
    }
    for( int i = 0; i < second.size_; ++i ) {
        newPoly.arr_[i] += second.arr_[i];
    }
    return newPoly;
}

多项式的乘法

　　在对多项式进行乘法运算时，我们可以使用乘法分配率：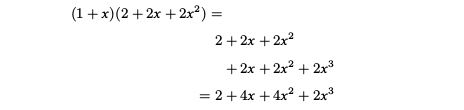

1
2
3
4
5
6
7
8
9
10
11
12
template <typename T>
Poly<T> multiply( const Poly<T> &first, const Poly<T> &second ) {
    int totalPower = ( first.size_ - 1 ) + ( second.size_ - 1 );
    Poly<T> newPoly( T{ 0 }, totalPower );
    for( int i = 0; i < first.size_; ++i ) {
        for( int j = 0; j < second.size_; ++j ) {
            newPoly.arr_[i + j] += first.arr_[i] * second.arr_[j];
        }
    }
    return newPoly;
}

多项式的求值

　　要是我们知道变量的值，那就可以对多项式进行求值了。例如可以直接对多项式进行求值：
$$
a_4x^4+a_3x^3+a_2x^2+a_1x+a_0
$$
　　可以发现，假定多项式的最高次幂是N，那么直接对多项式进行求值，计算复杂度是$O(N^2)$，然而，我们可以使用Horner算法，将计算复杂度降至$O(N)$，例如：
$$
a_4x^4+a_3x^3+a_2x^2+a_1x+a_0 = (((a_4x+a_3)x + a_2)x+a_1)x+a_0
$$
　　这样，对多项式进行求值只需要线性时间。

1
2
3
4
5
6
7
8
template <typename T>
double Poly<T>::evaluate( double value ) const {
    double result = 0.0;
    for( int i = size_ - 1; i >= 0; --i ) {
        result = result * value + arr_[i];
    }
    return result;
}

　　我们可以编写一个测试程序，验证以下多项式乘法：
$$
(1+x+\frac{x^2}{2}-\frac{x^3}{6})(1+x+x^2+x^3) = 1 + \frac{x^2}{2} + \frac{x^3}{3} - \frac{2x^4}{3} + \frac{x^5}{3} - \frac{x^6}{6}
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int main(int argc, char *argv[])
{
    auto poly1 = plus( Poly<double>( 1, 0 ), 
                       plus( Poly<double>( -1, 1 ), 
                             plus( Poly<double>( 0.5, 2 ), 
                                   Poly<double>( -1.0/6.0, 3 ) ) ) );
    auto poly2 = plus( Poly<double>( 1, 0 ),
                       plus( Poly<double>( 1, 1 ),
                             plus( Poly<double>( 1, 2 ),
                                   Poly<double>( 1, 3 ) ) ) );
    auto poly = multiply( poly1, poly2 );
    std::cout << poly << std::endl;
    int x = 2;
    std::cout << "if x is " << x << ", and result is " << poly.evaluate( x ) << std::endl;
    return 0;
}

　　程序的运行输出：

参考资料

Algorithms in C++ 3rd Edition by Robert Sedgewick