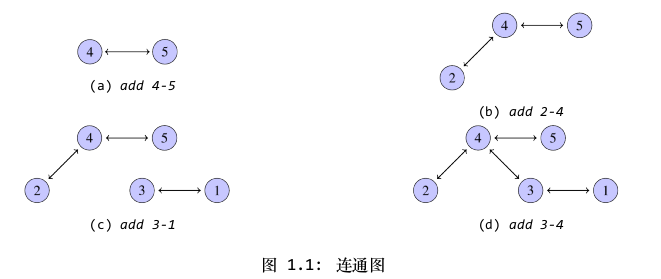
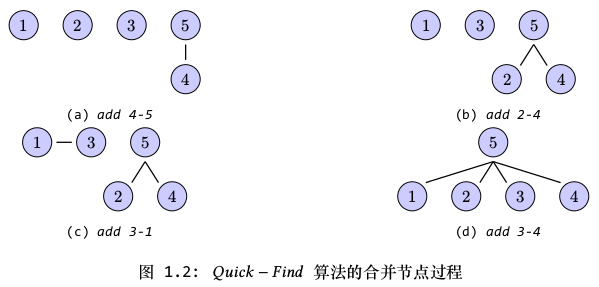
共享所有权

　　一个动态分配的对象可以在多个shared_ptr之间共享，这是因为shared_ptr支持 copy 操作：

1
2

shared_ptr<string> ptr1{ new string("hello") };
auto ptr2 = ptr1;　// copy constructor

原理介绍

　　shared_ptr内部包含两个指针，一个指向对象，另一个指向控制块(control block)，控制块中包含一个引用计数和其它一些数据。由于这个控制块需要在多个shared_ptr之间共享，所以它也是存在于 heap 中的。shared_ptr对象本身是线程安全的，也就是说shared_ptr的引用计数增加和减少的操作都是原子的。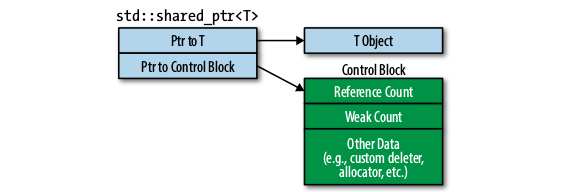

　　通过unique_ptr来构造shared_ptr是可行的：

1
2

unique_ptr<string> p1{ new string("senlin") };
shared_ptr<string> p2{ std::move(p1) };

shared_ptr 的风险

　　你大概觉得使用智能指针就再也高枕无忧了，不再为内存泄露烦恼了。然而梦想总是美好的，使用shared_ptr时，不可避免地会遇到循环引用的情况，这样容易导致内存泄露。循环引用就像下图所示，通过shared_ptr创建的两个对象，同时它们的内部均包含shared_ptr指向对方。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

// 一段内存泄露的代码
struct Son;
struct Father　{
    shared_ptr<Son> son_;
};
struct Son {
    shared_ptr<Father> father_;
};
int main() 
{
    auto father = make_shared<Father>();
    auto son = make_shared<Son>();
    father->son_ = son;
    son->father_ = father;
  
    return 0;
}

　　分析一下main函数是如何退出的，一切就都明了：

• main函数退出之前，Father和Son对象的引用计数都是2。
• son指针销毁，这时Son对象的引用计数是1。
• father指针销毁，这时Father对象的引用计数是1。
• 由于Father对象和Son对象的引用计数都是1，这两个对象都不会被销毁，从而发生内存泄露。

　　为避免循环引用导致的内存泄露，就需要使用weak_ptr，weak_ptr并不拥有其指向的对象，也就是说，让weak_ptr指向shared_ptr所指向对象，对象的引用计数并不会增加：

1
2
3

auto ptr = make_shared<string>("senlin");
weak_ptr<string> wp1{ ptr };
cout << "use count: " << ptr.use_count() << endl;// use count: 1

从异常安全说起

　　使用 raw pointer 管理动态内存时，经常会遇到这样的问题：

• 忘记delete内存，造成内存泄露。
• 出现异常时，不会执行delete，造成内存泄露。

　　下面的代码解释了，当一个操作发生异常时，会导致delete不会被执行：

1
2
3
4
5
6
7
8
9

void func() 
{
    auto ptr = new Widget;
    // 执行一个会抛出异常的操作
    func_throw_exception();
    
    delete ptr;
}

　　在 C++98 中我们需要用一种笨拙的方式，写出异常安全的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

void func() 
{
    auto ptr = new Widget;
    try {
        func_throw_exception();
    }
    catch(...) {
        delete ptr;
        throw; 
    }
    delete ptr;
}

　　使用智能指针能轻易写出异常安全的代码，因为当对象退出作用域时，智能指针将自动调用对象的析构函数，避免内存泄露：

1
2
3
4
5
6

void func() 
{
    std::unique_ptr<Widget> ptr{ new Widget };
    func_throw_exception();
}

unique_ptr 的原理

　　让我们了解一下unique_ptr的实现细节：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

namespace std {
    template <typename T, typename D = default_delete<T>>
    class unique_ptr
    {
    public:
        explicit unique_ptr(pointer p) noexcept;
        ~unique_ptr() noexcept;    
	T& operator*() const;
        T* operator->() const noexcept;
	unique_ptr(const unique_ptr &) = delete;
        unique_ptr& operator=(const unique_ptr &) = delete;
	unique_ptr(unique_ptr &&) noexcept;
	unique_ptr& operator=(unique_ptr &&) noexcept;
	// ...
    private:
        pointer __ptr;
    };
}

　　从上面的代码中，我们可以了解到：

• unique_ptr内部存储一个 raw pointer，当unique_ptr析构时，它的析构函数将会负责析构它持有的对象。
• unique_ptr提供了operator*()和operator->()成员函数，像 raw pointer 一样，我们可以使用*解引用unique_ptr，使用->来访问unique_ptr所持有对象的成员。
• unique_ptr并不提供 copy 操作，这是为了防止多个unique_ptr指向同一对象。
• 但unique_ptr提供了 move 操作，因此我们可以用std::move()来转移unique_ptr。

预留足够空间

　　vector实际上是能够动态增长的数组，因此，当vector的容量 ( capacity ) 不足以容纳新元素的时候，vecvtor就会重新分配较大的内存，将原来的元素移动到新的内存，并回收旧的内存。这个过程会导致几个问题：

• 每一次重新分配内存的操作都会带来不小的开销。
• 由于旧的内存被系统回收，因此，原来所有指向vector元素的指针、迭代器和引用都会失效。

　　每一次使用push_back()往vector中增加元素，可能会导致vector重新分配内存：

1
2
3
4
5
6
7
8
9
10
11

std::vector<int> vec;
auto cap = vec.capacity();
std::cout << "origin capacity: " << cap << std::endl;
for( int i = 0; i < 1000; ++i ) {
    vec.push_back( i );
    if( cap != vec.capacity() ) {
        cap = vec.capacity();
        std::cout << "new capacity: " << cap << std::endl;
    }
}

　　从例子可以看到，往vector中增加 1000 个元素，会导致vector多次重新分配内存：

1
2
3
4
5
6
7
8
9
10
11
12

origin capacity: 0
new capacity: 1
new capacity: 2
new capacity: 4
new capacity: 8
new capacity: 16
new capacity: 32
new capacity: 64
new capacity: 128
new capacity: 256
new capacity: 512
new capacity: 1024

　　为了减少重新分配内存带来的开销，实际上我们可以使用v.reserve(n)来预留足够的内存( v是vector的对象 )：

• 要是n小于或等于v.capacity()，那么，v将忽略这个操作。
• 要是n大于v.capacity()，那么，v将会重新分配内存，并保证新的容量至少为n。

　　很明显，要是一开始vector就预留足够的空间，那么，即使不断地使用push_back()增加元素，vector也不会重新分配内存，并且所有指向元素的指针、迭代器和引用仍然有效。需要明白一点，reserve()使用空间置配器 ( allocator ) 来分配内存，也就是，没有存储元素的那部分内存是原生 ( raw ) 内存。

　　根据这个方法，可以减少重新分配内存的次数：

1
2
3
4
5
6
7
8
9

const int NUM = 1000;
std::vector<int> vec;
vec.reserve( NUM );
std::cout << "origin capacity: " << vec.capacity() << std::endl;
for( int i = 0; i < NUM; ++i ) {
    vec.push_back( i );
}
std::cout << "new capacity: " << vec.capacity() << std::endl;

　　在数值计算中，有时我们需要对多项式进行相加或相乘，此外，还经常需要对多项式进行求值。例如，假定我们需要对两个多项式进行乘法运算：
$$
(1+x+\frac{x^2}{2}-\frac{x^3}{6}) (1+x+x^2+x^3)= 1 + \frac{x^2}{2} + \frac{x^3}{3} - \frac{2x^4}{3} + \frac{x^5}{3} - \frac{x^6}{3}
$$

多项式的表示

　　我们可以定义一个Poly类用来表示多项式，在Poly中，我们使用数组来存储多项式的系数，由于系数作为数组的元素，那么系数对应的下标就是多项式的幂，例如，假定我们使用Poly来表示多项式$5+10x+8x^2+20x^4$，那么数组的结构就如下图所示：

　　我们可以用Poly来表示多项式，例如，我们可以用Poly<int>(2, 2)来表示$2x^2$，当然，我们可以通过全局函数plus()来组合多项式，例如：

1

auto poly = plus(Poly<double>(0.5, 2), Poly<double>(9.9, 4));

　　那么，可以看到，poly就可以用来表示$0.5x^2 + 9.9x^4$，这时，若需要对多项式进行求值，例如，令$x=2$，那么可以使用Poly的成员函数evaluate()来进行求值：

1

std::cout << poly.evaluate(2) << std::endl;　　　　　　　　　    // print 160.4

　　下面给出Poly的具体实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

#include <iostream>
#include <vector>
template <typename T>
class Poly
{
    template <typename Type>
    friend Poly<Type> plus( const Poly<Type> &, const Poly<Type> & );
    template <typename Type>
    friend Poly<Type> multiply( const Poly<Type> &, const Poly<Type> & );
    template <typename Type>
    friend std::ostream &operator<<( std::ostream &, const Poly<Type> & );
public:
    Poly( T coefficient, int power )
        : size_{ power + 1 }, arr_( size_, T{ 0 } ) {
            arr_[power] = coefficient;
    }
    
    double evaluate( double value ) const;
private:
    int size_;
    std::vector<T> arr_;
};
template <typename T>
std::ostream &operator<<( std::ostream &os, const Poly<T> &poly ) {
    for( int i = 0; i < poly.size_; ++i ) {
        if( poly.arr_[i] != 0 ) {
            os << poly.arr_[i] << "x^" << i 
               << ( i != poly.size_ - 1 ? " +" : "" ) << " ";   
        }
    }
    return os;
}

Union-Find算法

　　在一个连通网络中，如果存在链路，使得一个节点能通过这条链路到达另一个节点，那么我们就说这两个节点之间是连通的。在连通性问题中，通常需要判断给定的两个节点是否已经连通，这个过程称为查找(find)操作，此外，若两个点并没有连通，我们可以创建连通这两个节点的链路，从而使得这两个节点处于连通状态，这个过程称为合并(union)操作。在执行合并操作之后，网络处于新的连接状态，这时，我们就可以根据更新后的网络的状态，来判断给定的其它两个节点之间是否连通了。
　　为了简化处理，我们可以使用整数来给网络中的节点进行编号。首先，我们给出一个测试程序，程序每次都会要求用户输入一对整数，并且执行以下操作：

• 判断这对整数代表的节点是否处于连通状态，这就是查找操作。
• 若这两个点没有连通，那么执行合并操作，使得这两个点处于连通状态。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  #include "uf.hpp" #include <iostream> using namespace std; int main() { UnionFind uf(10000); // 10000 nodes int p, q; while (cin >> p >> q) { if (uf.find(p, q)) { cout << "connection " << p << "-" << q << " already exist!" << endl; } else { uf.unite(p, q); cout << "new connection: " << p << "-" << q << endl; } } return 0; }

　　我们可以使用简单的输入来测试程序，输入的两个整数代表两个节点，若这两个节点尚未连通，那么程序就会负责连通这两个点，若这两个点已经连通，则输出提示信息：

1
2
3
4
5
6
7
8
9
10
11
12

4 5
new connection: 4-5
2 4
new connection: 2-4
2 5
connection 2-5 already exist!
3 1
new connection: 3-1
3 4
new connection: 3-4
1 2
connection 1-2 already exist!

　　我们可以用下图1.1来表示对节点执行合并操作的过程，从中可以看到，节点之间的连通是具有传递性，最后，图中的5个节点都处于互通的状态：

Quick-Find算法

　　在Quick-Find算法中，我们使用数组来表示所有节点的集合，在一开始，数组中的元素的值各不相同，这表示所有的节点均不连通，很显然，要是数组中存在相同的元素值，那么就表示这些元素所代表节点是互通的。由此，判断两个节点是否连通(即查找操作)就变得相当简单，只需要判断数组中的这两项元素的值是否相同，相同就表示它们是连通的。此外，要是这两个节点(假设为A节点和B节点)并不连通，那么就要执行合并操作，这时我们需要遍历整个数组，使得所有与A节点连通的节点都与B节点连通。
　　Quick-Find算法中，查找操作的复杂度为O(1)，而合并操作的复杂度为O(N)，N表示数组的长度，即所有节点的数目。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class UnionFind
{
public:
    UnionFind(int n) 
        : num(n), arr(num)
    {
	iota(arr.begin(), arr.end(), 0);
    }
    
    bool find(int p, int q) const
    {
        return arr[p] == arr[q];
    }
    
    void unite(int p, int q)
    {
        if (!find(p, q))
	{
            int origin = arr[p];
            for (int i = 0; i < num; ++i)
	    {
                if (arr[i] == origin)
		{
                    arr[i] = arr[q];
                }
            } 
        }
    }
private:
    int num;    // number of nodes
    vector<int> arr;
};

　　图1.2表示了Quick-Find算法合并节点的过程，需要注意，节点中的数字表示节点的编号(即数组元素的下标)，而不是数组元素的值。执行一次合并操作，我们需要遍历所有节点。